Calculating the analemma
日行迹始末
(计算日行迹也算是我少年时期的梦想:我在初中时就想定量地解出曲线,在高一时曾经尝试过未果;最终我在高三时又想起了这个问题并轻松地完成了计算。这篇文章基于我高三时的计算以及大一时写的一篇微信推送)
日行迹(analemma) 指的是太阳一周年中每天同一时刻的位置所连成的轨迹。由于计时系统是和平太阳(假象的匀速运动的太阳)的运动对应的,日行迹也反映着真太阳与平太阳的偏差。

可以看到,日行迹呈一个上小下大的不对称的诡异8字形,太阳在二月时位于左下方,五月的时候位于右上方,八月的时候来到左上方,十一月时回到右下方(见下图)。
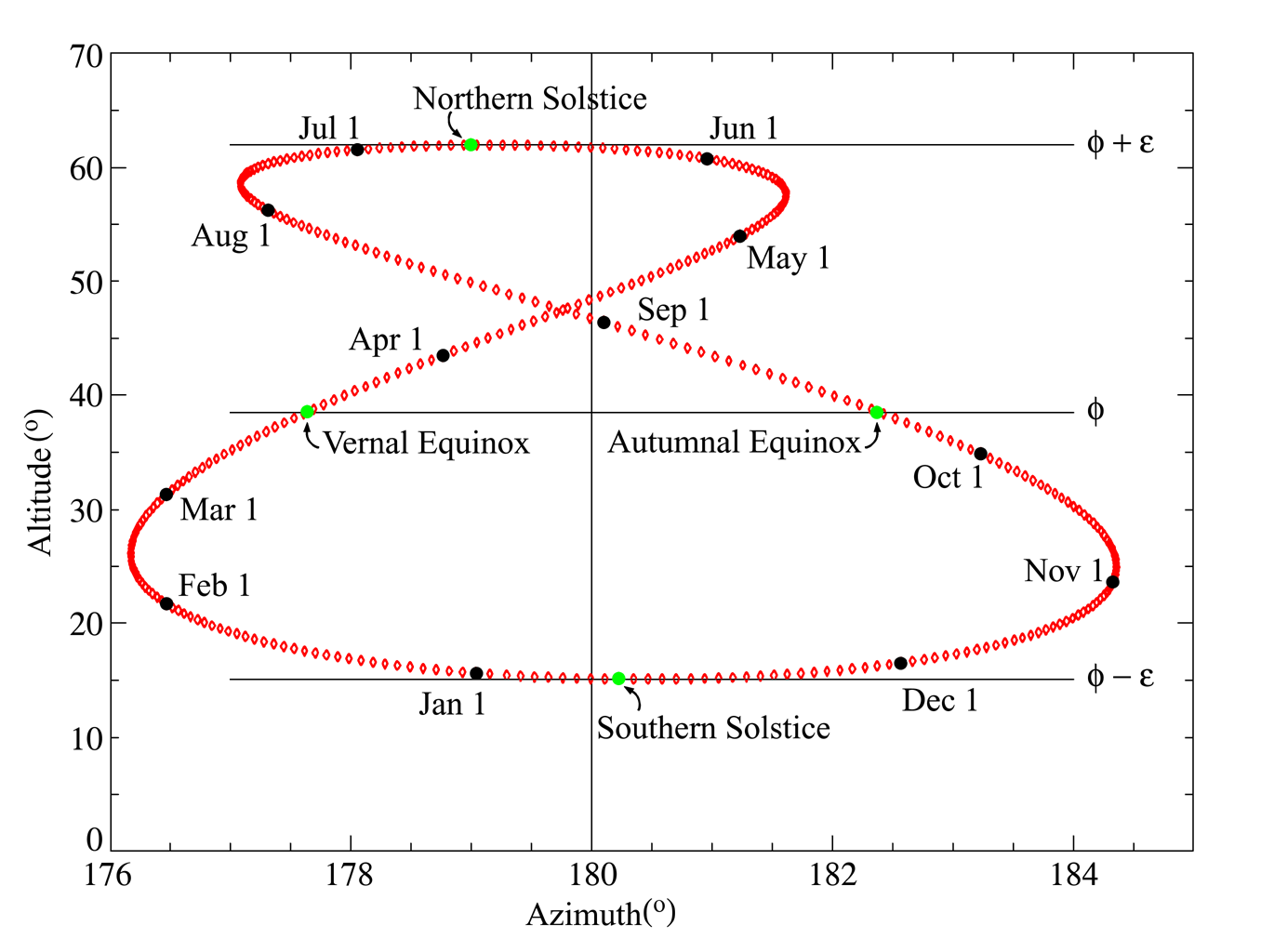
那么是什么因素导致了这个日行迹的奇怪形状呢?本篇文章中,笔者将尝试用理论计算的方式回答。
首先,如果太阳和平太阳的赤经运动速度相同,但是正午高度角会照常变化,那么每天正午的时候太阳也会准确地回到子午线上。这样的话,一年中太阳只会在子午线上上下折返,日行迹将是一条折线。这个……好像差的比较多。
我们接着考虑,太阳的赤经并不是匀速增加的。因为它在黄道上接近匀速地运动,黄经才应该是匀速增加的。而黄道和赤道并不重合,两者有个23.5°的夹角。
在这种假设下,我们再来考虑一下日行迹的形状。由太阳引“垂线”到天赤道上,利用球面三角的正弦和余弦定理,可以得到下图的两个公式。

接着可以得到 $\alpha=\cos^{-1}\left(\frac{\cos\lambda}{\sqrt{1-\sin^2\varepsilon\sin^2\lambda}}\right)$,$\delta = \sin ^{-1}\left(\sin \varepsilon \sin \lambda\right)$ 。我们假设地球匀速公转,所以$\lambda=\frac{T}{T_0}\cdot 2\pi$($T$是春分日之后的天数)。这样我们就得到了每一天太阳的赤经和赤纬。而日行迹的纵轴差不多就是赤纬,横轴则可以用$\alpha-\frac{T}{T_0}\cdot 2\pi$。接下来用一个T向量交给Matlab君画图就好了~
我们得到的是一个对称的八字形,比折线好多了,可是还是和正版的日行迹不大一样。为什们呢?或许是因为地球的轨道是椭圆形,导致 随时间的变化不是均匀的。椭圆的极坐标方程(以焦点为原点)是: \(r(\lambda ) = \frac{\left( {1 - e^2} \right)a}{1 - e\cos \left( \lambda - \lambda_0 \right)}\) ($\lambda_0$表示远日点时的黄经)。利用角动量守恒,
\[\omega \left( \lambda \right) = \frac{ {\rm d}\lambda }{ {\rm d} T} = \frac{v_0 \cdot \left( 1 + e \right)a}{r\left( \lambda \right)^2} = \frac{v_0 \cdot \left( 1 + e \right)}{\left( 1 - e^2 \right)^2a} \cdot \left( 1 - e\cos \left( \lambda - \lambda_0 \right) \right)^2\]诸君莫慌,实际上地球的偏心率很小(e=0.0167),所以我们可以一言不合把原来的方程泰勒展开,扔掉二阶以上的项。于是我们得到
这个东西是可以得到解析解哒(取倒数直接积分就好了)。最终我们开心地解得
\[\lambda - {\lambda_0} = 2\arctan \left[ \frac{\sqrt {1 + 2e} \tan \left( {\frac{v_0\left( {T - C} \right)}{2a}\sqrt {1 + 2e} } \right)}{3e + 1}\right]\]我们可以继续扔掉$e$的二阶项,最终将得到:
\[\lambda= {\lambda_0} + 2\arctan \left[ \frac{\tan \left( {\frac{v_0\left( {T - C} \right)}{2a}\sqrt {1 + 2e} }\left(1+e\right)\right)}{1+2e}\right]\]里面的$C$是积分常数,可以求得它是远日点在春分日之后的天数,大约是105天。 得到了$\lambda$之后,可以用之前一样的公式得到$\alpha$和$\delta$。同样地,我们还是把它交给Matlab君进行绘图(仍然是$\delta$-$\alpha-\frac{T}{T_0}\cdot 2\pi$)。
可以看到,考虑了离心率的一阶项之后,计算得到的理论日行迹有了不对称、上小下大的基本特征,和实际已经很接近啦。
由此可以看到,造成日行迹的主要原因就是:1、黄赤交角的存在;2、地球轨道的偏心率。当然,除了这二者以外,肯定还有章动、月球和其他天体对地球摄动等等笔者没有考虑进来(也不知道如何考虑进来)的因素,不过看起来它们对日行迹形状的影响都是微小的。